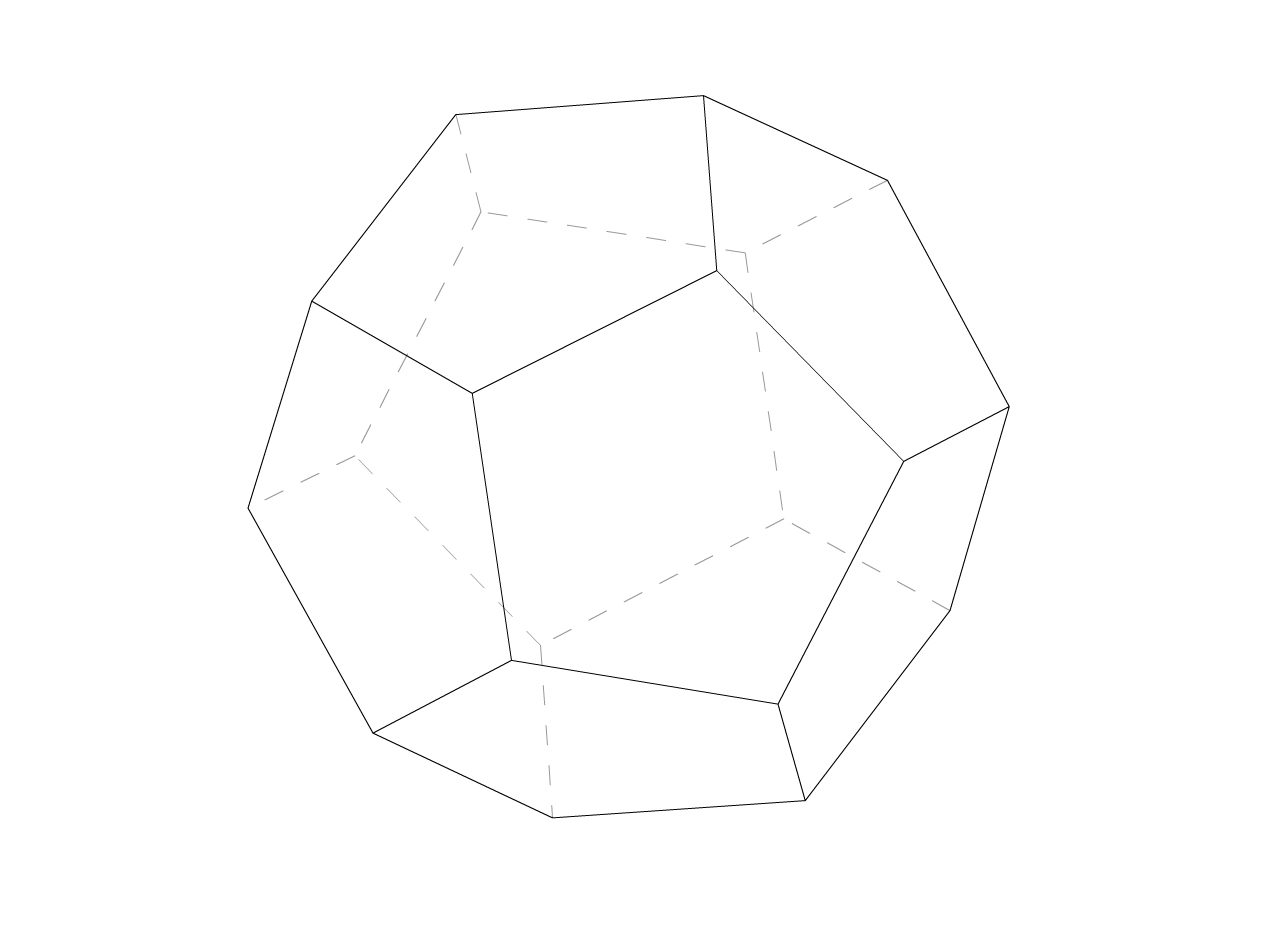
正四面体のポイントは!正四面体の体積の求め方!1底面となる正三角形abcの面積を求める!2oから 底面に下した垂線の足 h が底面の外接第4節正多面体と等面多面体(1) 1正12面体 ここでは,正12面体及び正面体の体積を求めます. 正多面体を扱いときは,実際に立体を手にとることが出来ないと,きちんとした理解が出来ません.1 正多面体 11 座標空間で考察 頂点を座標で表して考える。 111 正四面体 頂点 4 個 ( 1, 1, 1) (ただし, が奇数個) p1( 1, 1, 1), p2( 1,1,1), p3(1, 1,1), p4(1,1, 1) 面 4 個(正三角形) p1p4p3, p1p3p2, p1p2p4, p2p3p4 辺 6 個 辺の長さ 2 √ 2 面の中心 (1 3, 1 3, 1 3) (ただし,が奇数個)辺の長さが 2 p 2 3 の正四面体の
48s96ub7b0z5f Net Bunkatsu Taiseki
立方体 正四面体 体積比
立方体 正四面体 体積比-1 辺の長さが 2 cm の正四面体 a と,1 辺の長さが 3 cm の正四面体 b があ る。このとき,正四面体 a と正四面体 b の体積比を求めなさい。 右の図のように,ßabc の辺 bc 上に点 d, 線分 ad 上に点 e をそれぞれ ae ed = 2 1 , bd dc = 3 4 となるようにとる。直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の




高中数学空间几何体的外接球问题探究 每日头条
体積= 4 3 πr3 表面積=4πr2 2 立体の求積 ⑴ 底面は長方形ACGE,高 さはBDの 1 2 の長さになる。 ⑵ 3 相似比と体積比 底面積,高さと体積比 ① 底面積が同じ⇨体積比 は高さの比に等しい。 ② 高さが同じ⇨体積比は 底面積の比に等しい。 相似な立体の体積比2,四面体で同じようにできるのか 正四面体で考えてみましょう。正四面体の各辺を2倍にします。 同じ大きさの正四面体を何個か作ります。それを並べてみます。体積比は1 3 :2 3 =1:8ですから、8個の正四面体が入るはずです。 四面体{abcdと四面体pbcdの体積比は底面積bcdが等しいから,\ 高さの比{afpf}に等しい} (四面体{pcda})=16vと求めた本解は,\ {pcda\ →\ abcd}の流れで求めたスマートな記述である これが難しいと感じるならば,\ 無理をせず{底面積の比と高さの比を別々に考える}とよい
テーマ: 解答集 答1 十二面体の体積 1辺の長さが 3 で 対角線の長さの比が 1:√2 である菱形 12枚でできる十二面体の体積は? 十二面体の頂点には菱形の鋭角は4個,菱形の鈍角は3個集まっています。 解答1 菱形を4個の直角三角形に分けたら、辺の第5問 正四面体の求積 図形ドリル 6年生 正四面体 立方体 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 一辺が2の正四面体 = 一辺が1の正四面体が4つ 一辺が1の正八面体が1つ 一辺が1の正四面体の体積をVとすれば、一辺が2の正四面体の体積は2の3乗倍となる8Vなので、上の関係より 一 辺 が 1 の 正 八 面 体 の 体 積 = 8V − V × 4 = 4V
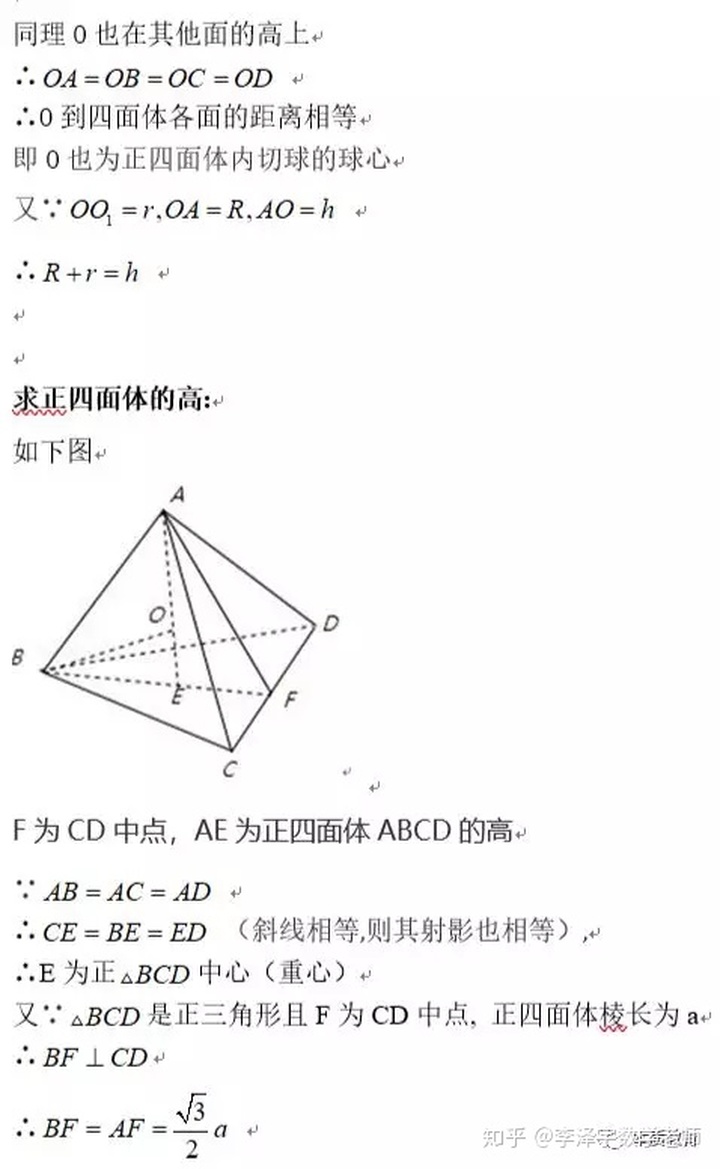
四面体は、既存の5つの正多面体のうちの1つです。 面が正多角形である多面体。 四面体は、正三角形である4つの辺、6つの辺、および4つの頂点で構成されています。 命令 1 四面体の一般式と正四面体の式の両方を使用して、四面体の体積を正しく計算でき答12 十面体の体積 1辺が8の正三角形の面だけでできる、図のような展開図をもつ 十面体の体積は? なお、この展開図で2種類の十面体が考えられます。Page 3 内接球の半径 半径 ri は点o から ∆abc および ∆bcd を含む平面までの距離 より,oh hk, である. 6 3 dh a= ,do oh 31= 以上より, 1 6 i 4 12 r oh dh a= = = 辺に接する球の半径 半径 re は,辺da および辺bc m( ) までの距離より,on om, である.すなわち,mn は辺に接する球の直径ということに




正立方體與正三角錐 1 Youtube




高校受験 中学数学 正四面体と体積比 Youtube
よって、正四面体の体積は、 \(\sqrt{2}×1×\displaystyle \frac{1}{3}×2=\displaystyle \frac{2\sqrt{2}}{3}(cm^3)\) と求まります。 立方体の中に正四面体 さらにもう \(1\) つ。 もっとも簡単に求める方法です。 ここでは、公式の導出をしてみましょう。 1辺aの正四面体の長さ・面積・体積・2平面のなす角度などまとめ 更新日: 年12月6日 公開日: 18年2月14日 2次試験対策 上野竜生です。 1辺がaの正四面体の長さや表面積などに関するものを求めてみました。 比較的求めやすいもの・試験問題に出 このとき次の問いに答えよ。 ただし正四面体の頂点から底面の三角形に引いた垂線と底面の交点は、底面の三角形の外接円の中心であることは証明無しで用いてよい。 (1)正四面体qの1辺の長さを求めよ (2)球pと正四面体qの体積比を求めよ。



48s96ub7b0z5f Net Bunkatsu Taiseki



48s96ub7b0z5f Net Bunkatsu Taiseki
3 正多面体の表面積・体積 34 正十二面体 ¶ ‡ 例題332 1 辺a の正八面体の体積va を求めよ。 µ a b d c e o f 図21 正八面体の体積 1 辺1 の体積v1 を求める。 正八面体は3 つの正方形が互いに直交して 作られる構造だということを理解していると 簡単である。図でいえば,四角形abfd,四問 四面体 abcd の内部にある点 p が2ap 3bp 4cp 5dp = 0 を満たすとき,四面体 pbcd, pcda,pdab,pabc の体積比を求めよ.< 2 つの解法><この問題に体積比は 4× 2 4 3 4 3 9× 211 3 = 14 27 である.三角柱ajkbnm の体積は四面体abcd の半分だから三角柱aj1k1bn1m1 と四面体 abcd の体積比は7 27 と分かる. メビオ2巡目テキスト 1 辺の長さ1 の正四面体の4 つの頂点をa0, b0, c0, d0 とする.この正四面体の各面 a0b0c0, a0b0d0, a0c0d0, b0c0d0 の重心をそれぞれd1




原创 新高考 21届高三精准培优专练14 与球有关的组合体下载 Word模板 爱问共享资料



正四面体体积 万图壁纸网
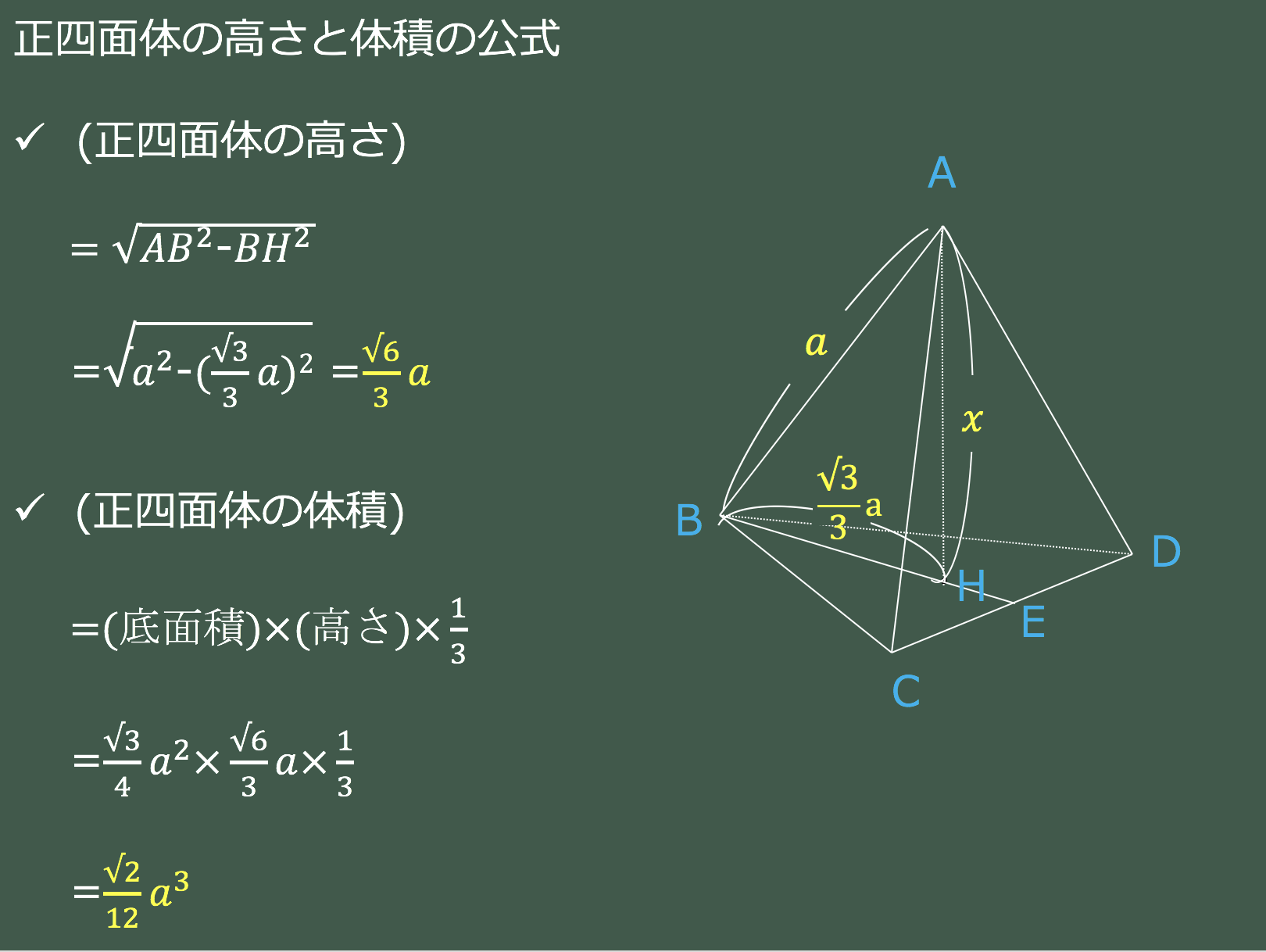
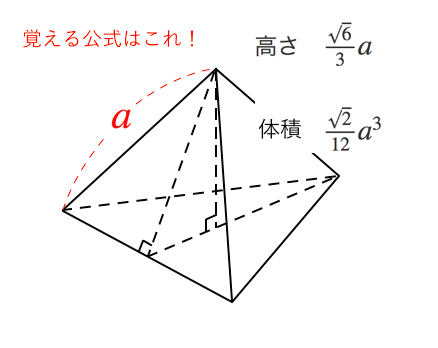
これから、この正四面体の体積は 1 3 × √3a2 4 × √6a 3 = √2 12 a3 1 3 × 3 a 2 4 × 6 a 3 = 2 12 a 3 と求めることができます。 3}四面体の底面積は,\ 平行六面体の底面積の\ 12\ である (三角錐)=(底面積)(高さ)13\ より,\ (四面体の体積)=(平行六面体の体積)16\ となる 高校範囲で4点の座標から四面体の体積を求めるには,\ かなり面倒な計算が必要であった四 面体 pqrs は pq = qr = rs = sp より ここ で ad = ac = ル と する と n 7 0 より ltfe 正 四 面体 で 、 abcd と 相似 と なる 。 (つ けい) こ r = つ に i 相似 比 は pq に cd = pq に ab = に 3 つし た が 1 ad = the よ、 て pqrs の 体積 は abcd の 体積 の) に x1 = o 2 は な set さ) に




正四面體 正四面體是由四個全等正三角形圍成的空間封閉圖形 所有棱長都相等 百科知識中文網
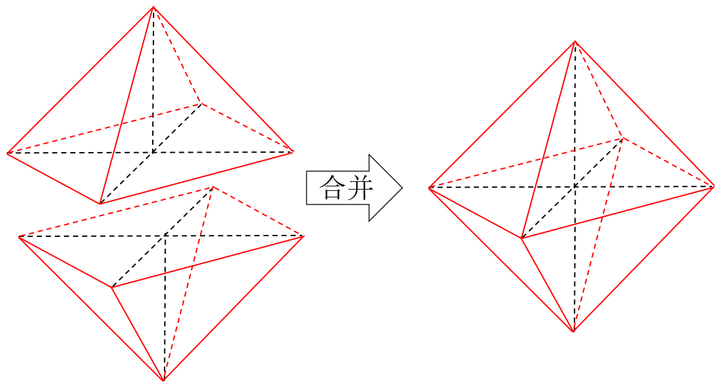



为什么正八面体体积是正四面体体积4倍 知乎
数学・算数 正四面体 角度 氷では、 正四面体の中心に酸素があるとして4つの頂点には 水素があります。 現実の氷ではなく、純粋な数学的に幾何学的に その酸素と水素の間の角度は、何度になるのでしょ 質問No(2) 正四面体acfhの体積を直接出すことは無理なので、 立方体から、いらない部分を引き算して求める。 いらない部分は全て同じ形の三角錐である。空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m2 n2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底



不规则四面体知道六边的体积公式 一个蒟蒻的蜕变之路 Csdn博客




直角四面体面积公式推导 北冥 的博客 程序员宅基地 直角四面体体积公式 程序员宅基地
正四面体の一辺をaとすると, 高さ である.=1633 である. c sin 2 3 cos 1 3, 547 = = = ° m m m θ θ θ ()a a a m m3-2.珪酸塩鉱物の分類とSiO4四面体の連結方式 目次: このように、SiO4四面体は非常に強固な構造を持つがゆえに、通常の金属酸化物とは異なり、SiO4四面体を骨組みとする珪酸塩鉱物は特殊な結晶構造を持つようになる。 その大きな理由としては、SiO4四面体が、溶融体や高温の熱水中では珪酸 図から、正四面体の1つの面(三角形)の面積S/4は、 2 体積V=底面積×高さ/3 リンク; 三角錐の体積の公式 三角錐の重心(四面体の重心) 正四面体に外接する球の半径R 正四面体に内接する球の半径r 正四面体の面が交差する角度 リンク:高校数学の



四面体外接球体积问题 文章阅读中心 急不急图文 Jpjww Com




22高三数学第一轮复习 空间几何体的表面积与体积公式大全 升学 恒艾教育
三角錐の重心(四面体の重心) 正四面体の高さと表面積と体積V 正四面体に外接する球の半径R 正四面体に内接する球の半径r 正四面体の面が交差する角度 三角形の内角の和が180のやさしい証明 やさしい三平方の定理の証明 中学数学の目次 高校数学練習問題 正四面体 を の ところで,底面に平行な平面で切ると,小さな正四面体 ができます。 以下の問いに答えなさい。 (1) 正四面体 と正四面体 の表面積の比を求めよ。 (2) 正四面体 と正四面体 の体積の比を求めよ。 練習問題 解答へ 数学Ⅰの目次へ



正八面体 正四面体的有趣问题



正八面体 正四面体的有趣问题
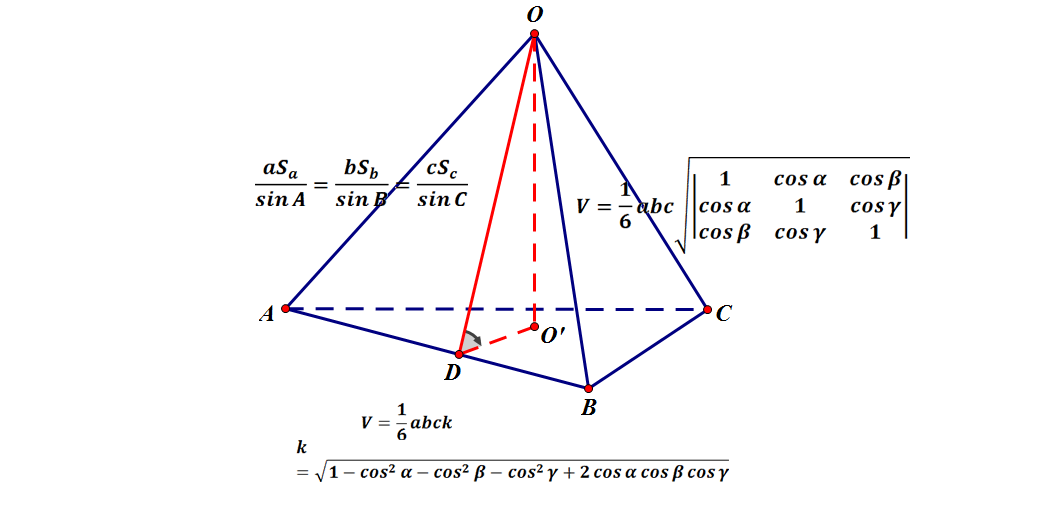



四面体体积公式 知乎




阳友雄 正四面体性质及其应用 网易订阅



四面体外接球体积问题 文章阅读中心 急不急图文 Jpjww Com



试题3 1 3空间几何体的表面积与体积 1 3空间几何体的表面积与体积 高中人教a版 数学中国网




正四面体の体積の求め方 3 Youtube



有关正八面体 正四面体的有趣问题 棱锥
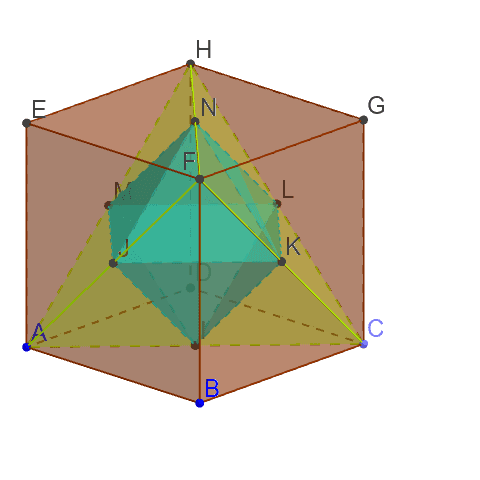



正四面體 正六面體 正八面體 Geogebra




2 の四面体aefdの体積と 正四面体abcdの体積比の求め方がわからない 中学校 教えて Goo




高中数学空间几何体的外接球问题探究 每日头条



四面体外接球体积问题 文章阅读中心 急不急图文 Jpjww Com




过四面体对边中点的平面 过正四面体一边及对边中点的截面把四面体分成两部分的体积之比为 A 1 2b 1 1c 1 4d 三人行教育网 Www 3rxing Org



近期模拟卷中整理出的九个还不错的题目 教育资讯 电影风云娱乐网



四面体外接球体积问题 文章阅读中心 急不急图文 Jpjww Com



正方体与正四面体 Seatop Com Cn



正四面体体积 万图壁纸网




四面體 維基百科 自由的百科全書
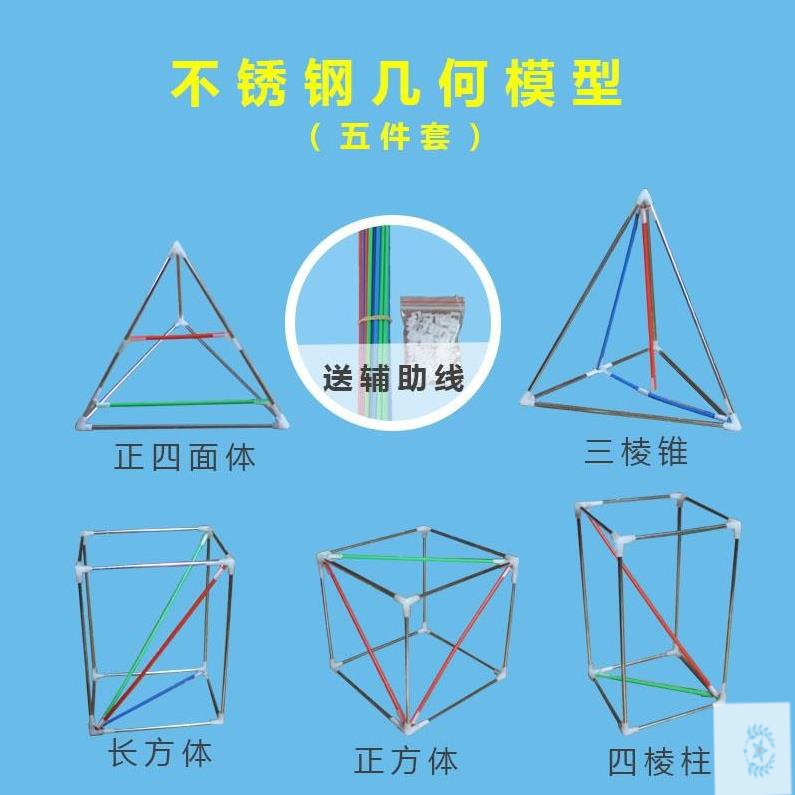



圆柱圆锥体积比 新人首单立减十元 21年8月 淘宝海外



空间几何体的表面积与体积公式大全下载 Word模板 爱问共享资料



四面体外接球体积问题 文章阅读中心 急不急图文 Jpjww Com




四面体的表面积 正四面体探究式学习 宇宙探索未解之迷的博客 Csdn博客



必修2立体几何 正四面体内切外接球问题 巧解之等体积法 哔哩哔哩 つロ干杯 Bilibili



3分で分かる 正四面体の高さ 体積の求め方をわかりやすく 合格サプリ




高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月




恒隆數學獎 To Infinity 無限可能 數造生活 點解粽係正四面體 粽嘅形狀通常係四面體 即係四面都係三角形 咁點解唔係六面體 十二面體 又或者球體呢 你今日食咗粽未呀




过四面体对边中点的平面 过正四面体一边及对边中点的截面把四面体分成两部分的体积之比为 A 1 2b 1 1c 1 4d 三人行教育网 Www 3rxing Org



正四面体的体积 哔哩哔哩 つロ干杯 Bilibili



四面体 信息图文欣赏 信息村 K0w0m Com



正八面体 正四面体的有趣问题




正四面体を平面で切断したあとの2つの立体の体積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




圆柱圆锥体积比 新人首单立减十元 21年7月 淘宝海外



正三棱锥外接球正四面体外接球和内切球的半径的求法 学习岛




端午别只知道吃 来看看粽子里面的几何学 每日头条



高校数学 正四面体 高さ 体積 オンライン無料塾 ターンナップ Youtube



正四面体外接球体积图 搜狗图片搜索



正四面體 维基百科 自由的百科全书




袋鼠数学竞赛真题及解析 三



若正方体的八个顶点中有四个恰好是正四面体的顶点 则正方体的表面积与正四面体的表面极之比是 数学作业 解题作业帮



正四面体体积 万图壁纸网




旋转四面体




18高考数学100弹之第53弹 正方体 雪花新闻



腾讯视频




2 を教えてください Clear




正四面体外接圆半径棱长为a的正四面体的内外接圆半径 求详细过程



四面体体积公式 知乎



正四面体三角錐 ニーアオートマタ壁紙



公务员联考直播冲刺班作业第28天 数量关系 国家公务员考试网



正四面体 搜狗百科



正四面体内 手机壁纸 电脑壁纸 桌面壁纸 图客网




高校数学 正四面体の高さと体積 例題編 映像授業のtry It トライイット



正四面体重心到顶点的距离与到对应地面的距离的比是多少 作业 慧海网




正四面体 全世界条目




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




高考数学 正三棱锥的内切球与外接球 壹读



四面体体积公式 四面体体积公式6分之一 正四面体体积公式



腾讯视频




正方体的8个顶点中 有4个恰是正四面体的顶点 则正方体与正四面体的表面积之比为 雨露学习互助



正八面体 正四面体的有趣问题




高校数学 対称面をもつ四面体の体積 受験の月



坐标求四面体体积 正十二面体体积推导 一 Weixin 的博客 程序员宅基地 程序员宅基地



有关正八面体 正四面体的有趣问题 棱锥



正四面体的体积 哔哩哔哩 つロ干杯 Bilibili




正四面体 Wikiwand



正四面体棱切球图示 万图壁纸网



多面体与球的内切 外接问题 探索新知 中学数学研习 微信公众号文章阅读 Wemp



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ



每日一题 1412 正四面体与圆锥面 Math173



正四面体的内切球图片 搜狗图片搜索



正四面体 高さ 面積を求める公式 苦手な数学を簡単に



四面体的表面积 那些让你加快解题速度的高中数学公式 28 利用公式解决正四面体内切球和外接球的问题 曼汉学院的博客 程序员宅基地




正四面體regular Tetrahedron 的高和邊長的關係 學校沒有教的數學 學校沒有教的數學




几何体的表面积和体积 静雅斋 51cto博客




正四面体与内切球表面积之比 已知一个正四面体中 第一个球是它的内切球 第二个球是它的外接球 求这两个球的表面积之比及体积之比 三人行教育网 Www 3rxing Org




球体与简单几何体的切接问题 静雅斋 51cto博客



正四面体体积 万图壁纸网
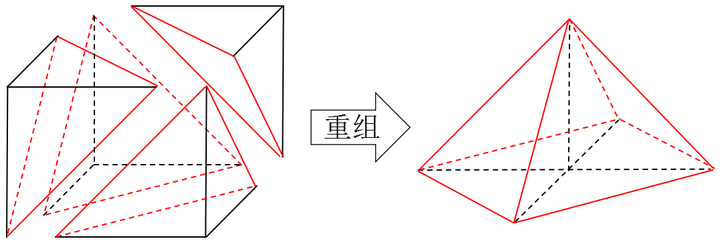



为什么正八面体体积是正四面体体积4倍 知乎
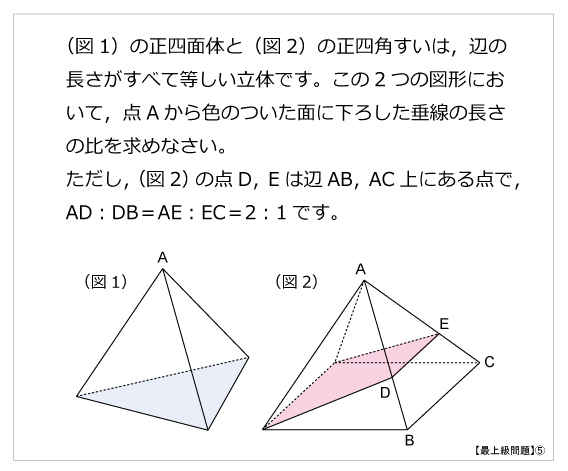



正四面体 算数星人のweb問題集 中学受験算数の問題に挑戦



四面體 維基百科 自由的百科全書



正四面体棱切球半径图 正四面体棱切球半径 江苏凤巢网络



正八面体と正四面体の体積比をカッコよく求める Roombaの日記




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



正四面體 维基百科 自由的百科全书




人力资源正三棱锥与正四面体体积及其计算下载 Word模板 爱问共享资料




正四面体 Wikiwand




高校数学 正四面体の高さと体積 練習編 映像授業のtry It トライイット



四面体的内切球图片 搜狗图片搜索




一个与四面体有关的古老问题 终于被证明了 柏拉图 多面体 立方体 多项式 网易订阅



0 件のコメント:
コメントを投稿